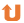■ Profile.別性能表
DESC
Profile とは Graphics 命令セットの種類のこと
C, C++ で Target Machine を指定するのと同じ
Cg Compiler にこの Hardware 用に Compile しろというのと同じ
WARNING
GPU によって利用できる命令セット, インストラクション数に限界がある
コンパイルができても Load で失敗する可能性がある
// foo.fsh(133) : error C5051: profile does not support conditional returns
cgc -arbfp1 foo.fsh
// vertex shader は tex2D 命令は support しない
// foo.fsh(176) : error C3004: function "tex2D" not supported in this profile
cgc -arbvp1 foo.fsh
■ 行列の積(mul)
POINT
Cg の mul は次の順番で処理される。
mul( m, v ) は以下の計算結果になる。
m00 m01 m02 vx m00*vx + m01*vy + m02*vz
m10 m11 m12 vy == m10*vx + m11*vy + m12*vz
m20 m21 m22 vz m20*vx + m21*vy + m22*vz
// Fragment Shader で確認できる
float3x3 m = {
{ 1, 1, 1 },
{ 0, 0, 0 },
{ 0, 0, 0 },
};
{
float3x3 m = {
{ 1, 0, 0 },
{ 1, 0, 0 },
{ 1, 0, 0 },
};
// 結果は白 ( 1, 1, 1 )になる。
return float4( mul( m, float3(1,1,1) ), 1 );
}
Model -> World -> View -> Projection
mul(m, IN.pos) mul(v, posW) mul( p, posV )
■ shader.コツ
Constant Register 数に気をつける
Matrix の積ではなく, dot ( 内積 )で代用する
命令数に気をつける
■ SYNTAX
POINT
global 変数として定義しても良い。
この方が, 関数の引数よりもテストしやすいので利用すること
// インクルード
#include "common.h"
// global として定義
uniform float scl = 1;
float4 main(
// 仮引数として定義
uniform float scl;
)
// #define
#define LIGHT_NUM 7
#ifdef _MAYA_
#else
#endif
// 引き数つきマクロ
#define LIGHT_DECLARE( N ) float4 light_ ## N
// C と同じく \ で複数行を連結する。
#define LIGHT_DECLARE( N ) float normalmap_scale ## N \
< \
UIName = "Nomalmap Scale" \
> = {0.1f}
■ 行列
// 成分のとり方
float3 v = m._m03_m13_m23;
// 1行目を取得。
float3 v = m[0];
かける順番
mul( m, v );
次のように構成だと考えられる
Ax Ay Az T
[00][01][02][03] (x) = (Xnew + Tx)
[10][11][12][13] (y) (yNew + Ty)
[20][21][22][23] (z) (zNew + Tz)
[30][31][32][33] (1) (1)
POINT
mul( m, v )は 次の計算
v.x = 0行目 ( m[0] ) * v
v.y = 1行目 ( m[1] ) * v
v.z = 2行目 ( m[2] ) * v
v.w = 3行目 ( m[3] ) * v
float4x4 m;
m[0] = float4(1,1,0,0);
m[1] = float4(0,1,0,0);
m[2] = float4(0,0,1,0);
m[3] = float4(0,0,0,1);
// { 1, 0.5, 0, 1 } == オレンジ色
float s = 0.5f;
OUT.col = mul( m, float4(s,s,0,1) );
// { 0.5, 1, 0, 1 } == ライトグリーン
m[0] = float4(1,0,0,0);
m[1] = float4(1,1,0,0);
m[2] = float4(0,0,1,0);
m[3] = float4(0,0,0,1);
OUT.col = mul( m, float4(s,s,0,1) );
// 成分指定 がどこを指すかチェック
m[0] = float4(1,0,0,0);
m[1] = float4(1,1,0,0);
m[2] = float4(0,0,1,0);
m[3] = float4(0,0,0,1);
m._m10 = 0; // 1行, 0 列
m._m11 = 0;
// { 0.5, 0, 0, 1 } Dark Red
float s = 0.5f;
OUT.col = mul( m, float4(s,s,0,1) );
行列スウィズル演算子
< type>< rows>x< columns> という形式の行列型の場合、
matrix._m< row>< col>
matrix._m< row>< col>[_m< row>< col>][...]
という表記法を使用して、個々の行列要素にアクセスしたり(< row>< col>ペアが1つのみの場合)
行列の要素からベクトルを構成したり(< row>< col>ペアが複数存在する場合)することができる。
行と列の番号は0 から始まる
// 連続で指定できる
// Assign the main diagonal of myMatrix to myFloatVec4.
fvec4 = myMatrix.m_00_m11_m22_m33;
float4x4 a と宣言したとすると、a[3] は a._m30_m31_m32_m33 に等しくなる
どちらの式も、行列の3 行目を取り出す
// Az 成分( 列 )をとる
float3 Az = m._m02_m12_m22;
// Cg Reference より抜粋
mul() は 3 つの使用方法がある。
行列 × 列ベクトル
mul(M, v);
行ベクトル × 行列
mul(v, M);
行列 × 行列
mul(M, N);
// 次のような 記述になる
(m11 m21 m31 m41) (v1)
(m12 m22 m32 m42) (v2)
(m13 m23 m33 m43) (v3)
(m14 m24 m34 m44) (v4)
float3 eyevec_w = viewI._m03_m13_m23 - pos_w;
OUT.test = float4( viewI._m03_m13_m23, 1.0f );
float3x3 nmatrix = float3x3( tan, bin, nml );
nmatrix[0] = tan;
nmatrix[1] = bin;
nmatrix[2] = nml;
float4 a = float4( 1.236812, -0.714074, -0.866025, -0.577350 );
float4 b = float4( 0.000000, 1.428148, -0.866025, -0.577350 );
float4 c = float4( -1.236812, -0.714074, -0.866025, -0.577350 );
float4 d = float4( 1.785185, 0.507938, -68.817703, 120.788200 );
// float4 から matrix 生成
float4x4 mtxLit = float4x4( a, b, c, d );
float4 a = float4(1,2,3,1);
return float4(a[0], a[1], a[2], 1 );
// 要素をえる( 0 行 0 列 )
float4x4 m;
float f = m[0][0];
■ Reference(Cg)
■ floor
SYNTAX
floor( f )
DESC
f 以下の最大の整数
浮動小数点 の 整数部 をとりだす
■ frac
SYNTAX
frac( f )
DESC
f の小数部
■ cross
SYNTAX
cross(float3 a, float3 b)
DESC
ベクトル a と b の外積
a から b への外積
a = 1, 0, 0
b = 0, 1, 0
0 0 1
0 0 1
-----
0 0 1
0 1 0
1 0 0
-----
0 0 0
1 0 0
0 1 0
-----
0 0 1
0 0 1
------
-1
c = a * b の定義 ( aからbまで回す右ねじの進む向き)
a.y*b.z + a.z * b.x + a.x + b.y
-
b.y*a.z + b.z*a.x + + b.x*a.y
float3 cross(float3 a, float3 b)
{
return a.yzx * b.zxy - a.zxy * b.yzx;
}
// fragment shader で試すと 青
return float4( cross( float3(1,0,0), float3(0,1,0) ), 1 );
// 黒
return float4( cross( float3(0,1,0), float3(1,0,0) ), 1 );
■ lerp
SYNTAX
lerp(a, b, f)
DESC
(1-f)*a + f*b
TIP
WARNING
描画結果が正しくない現象が見られる
自前で計算した方が無難
■ reflect
SYNTAX
floatN reflect( floatN i, floatN n);
DESC
param n: Normal ( 要 normalize )
param i: IncidentVector
WARNING
i は VtxPos - EyePos
Lighting 時とは逆向き の Vector
PROFILE
fp20
■ tex2Dproj
SYNTAX
tex2Dproj (sampler2D tex, float4 sq);
DESC
Texture 座標を W=1 の空間に変換後に sampling する
PROFILE
PS20
シャドウマップルックアップ:
テクスチャ座標のz 成分が、シャドウマップと比較する深度値を保持
シャドウマップルックアップでは
深度比較テクスチャリングのためにアプリケーションにより構成された関連テクスチャのユニットが必要
これがないと、深度比較は実際に実行されない
■ clamp
SYNTAX
clamp(x, a, b)
DESC
x < a = x = a
x > b = x = b
else x;
■ abs
SYNTAX
abs(x)
DESC
abs(x) x の絶対値
■ length
SYNTAX
float length( floatN vec )
DESC
vec の長さ( ノルム )を返す
float length( float3 vec ) {
return sqrt( dot(vec, vec) );
}
■ exp
SYNTAX
exp(x)
DESC
Euler ^ x
■ exp2
SYNTAX
exp2(x)
DESC
2^x
■ step
SYNTAX
floatN step( floatN a, floatN x)
DESC
x >= a となる階段関数で変換した値を返す。
■ normalize
SYNTAX
normalize(x)
DESC
N次元ベクトルを正規化する